Neural Collaborative Filtering 논문 리뷰
주요 내용
- 논문이 풀고자 하는 문제는 implicit feedback을 토대로 item을 user에게 추천하는 것
- deep learning을 matrix factorization에서 user-item interaction 부분에 적용하는 것
- dot-product(GMF)와 MLP의 장점을 모두 살린 네트워크 구조 사용
- loss function으로 MSE가 아닌 binary cross-entropy 사용
- point-wise loss + negative sampling 사용
- BPR과 eALS를 large-margin으로 outperform
→ 다른 유튜브 논문이나 wide and deep 논문에서는 여러 feature를 어떻게 잘 조합하느냐에 집중했음. 이 논문에서는 정말 collaborative filtering 세팅에 집중해서 다른 feature 없이 deep learning을 사용해 잘 학습하는 것에 집중함. 은근 참고할 내용이 많아서 꼭 한 번 읽어봐야 함.
implicit data 학습
- 추천 학계에서는 그동안 주로 explicit feedback으로 학습해왔는데 트렌드는 implicit feedback임
- implicit feedback은 자동적으로 데이터가 수집되고 데이터가 풍부하다는 게 장점
- 단점은 negative feedback의 부재. 사실 이 문제를 어떻게 해결하느냐가 implicit feedback 추천에서 제일 중요함. 사실 여기서 데이터는 positive vs negative가 아니라 observed vs unobserved 임. 중요함.
- 두 가지 objective function이 있는데 point-wise loss와 pair-wise loss가 있음
- BPR(Bayesian Personalized Ranking)에서는 pair-wise loss를 사용함.
- point-wise loss를 사용하는 Matrix factorization 모델 중에서 가장 SOTA는 eALS임. BPR 보다 좋음.
dot-product의 문제
- 잘 와닿지는 않지만 다음 그림으로 설명. user-item interaction matrix에서 user 끼리의 유사도를 측정함. u1, u2, u3에 대해 유사도에 따라 벡터를 그려보면 (이걸 latent factor라고 가정) (b) 그림과 같이 나옴. 새로 u4가 들어와서 u1, u2, u3와 유사도를 측정해보면 u1 > u3 > u2 순으로 u4와 유사함. 하지만 p4를 어디에 놔도 p3보다 p2가 더 가깝기 때문에 ranking loss가 커질 수 밖에 없음. dot-product가 linear 하기 때문에 발생하는 문제인데 그래서 non-linear인 neural net를 쓰겠다는 논리를 펼치는 것.
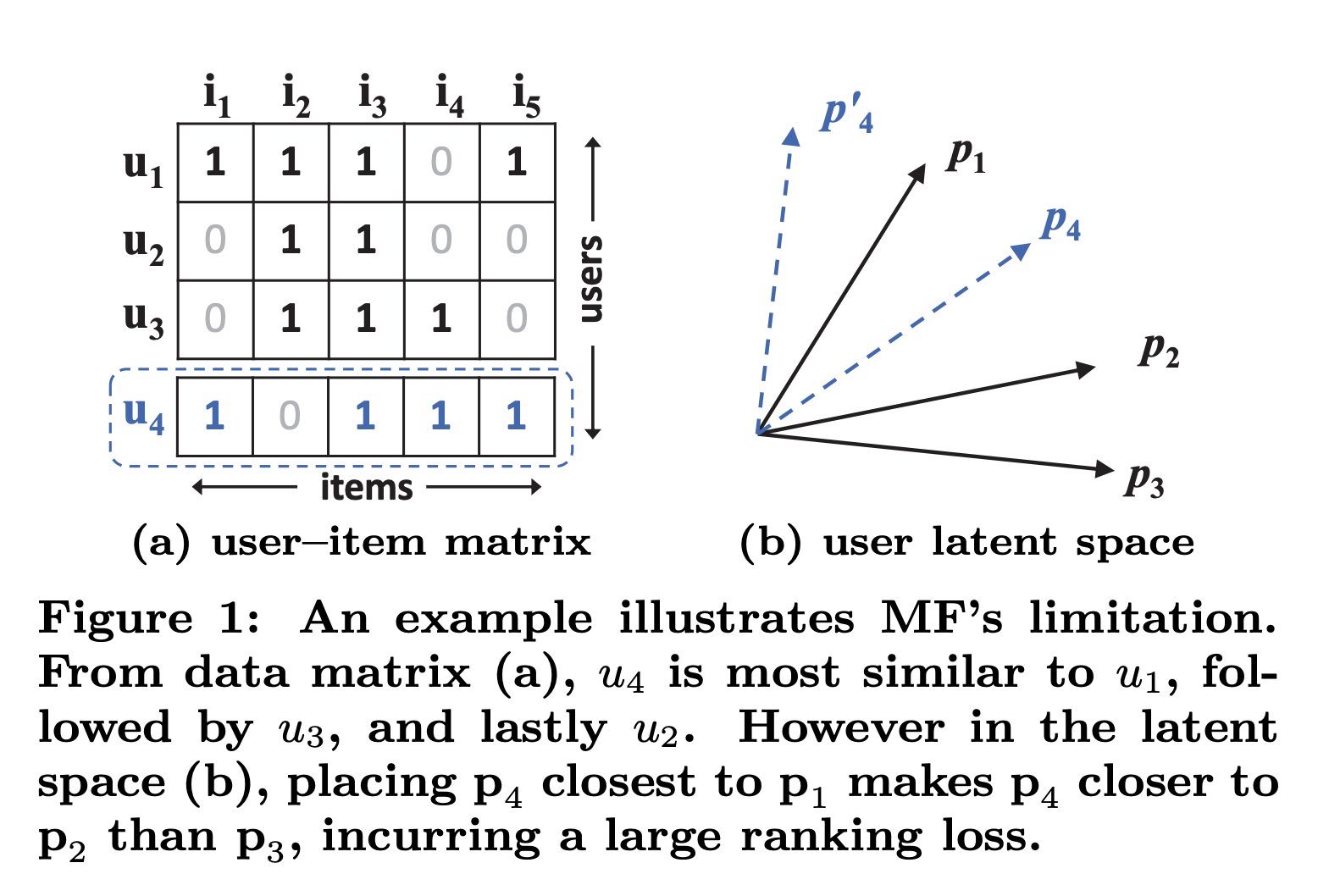
- 사실 위 문제는 latent factor의 dimension이 낮기 때문에 발생하는 문제인데 이 문제를 해결하기 위해 dimension을 높이면 오히려 overfitting이 발생함 → 그래서 latent factor의 dimension을 높이는 것이 아니라 user factor와 item factor 간의 상관관계를 풍부하게 표현하는 방향으로 생각을 바꿈.
Neural Collaborative Filtering Framework
NCF는 user latent factor와 item latent factor간의 상관관계를 표현하는데 MLP를 사용한다는 관점에서 다음과 같은 구조로 표현할 수 있음
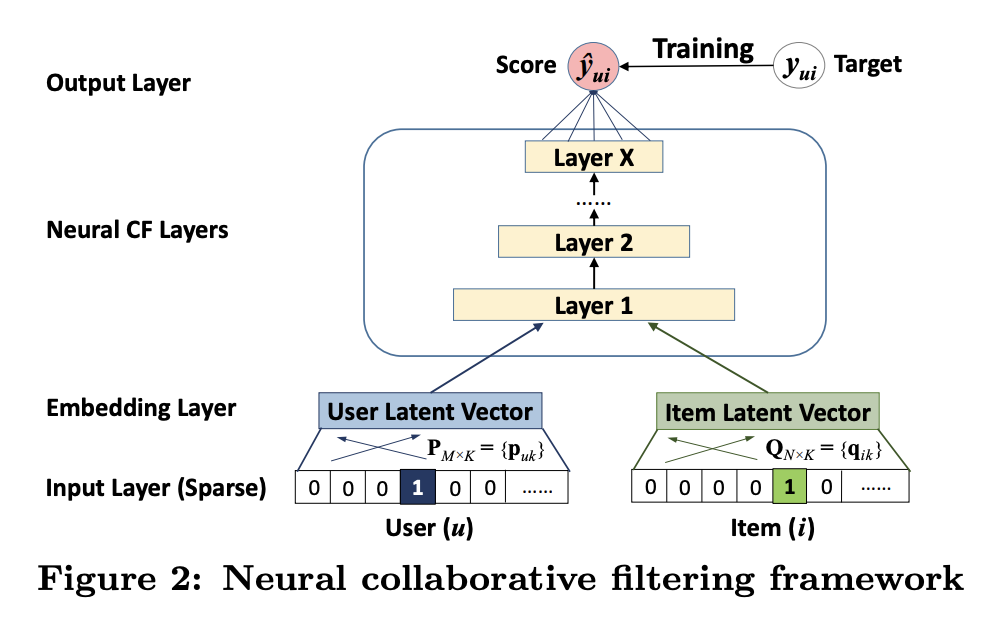
- user embedding과 item embedding을 latent factor로 보고 그 두 개의 vector를 뉴럴넷에 넣어서 이래저래 하는 것을 NCF라고 함.
- 원래 WMF에서는 loss function으로 MSE를 사용했는데 그건 output를 gaussian distribution으로 봤기 때문임. 하지만 정답은 1 또는 0 밖에 없기 때문에 가우시안이 아닌 probabilitic function을 사용하는 것이 좋음 (?? 이거 사실 이해 못함). 따라서 sigmoid function으로 output을 내보내고 loss function으로는 binary cross-entropy를 사용

- 학습은 SGD로
Generalized Matrix Factorization
- 줄여서 GMF. MF의 일반화 버전으로 MF에서는 단순 dot-product로만 output을 예측했다면 GMF에서는 element마다의 weight를 학습함. p와 q가 embedding인데 두 embedding을 element-wise로 곱한 다음에 weight를 곱함. 그리고 non-linear activation function을 사용해서 모델이 user-item interaction을 더 풍부하게 표현할 수 있도록 함. h가 uniform vector이고 a가 1이면 그게 바로 MF
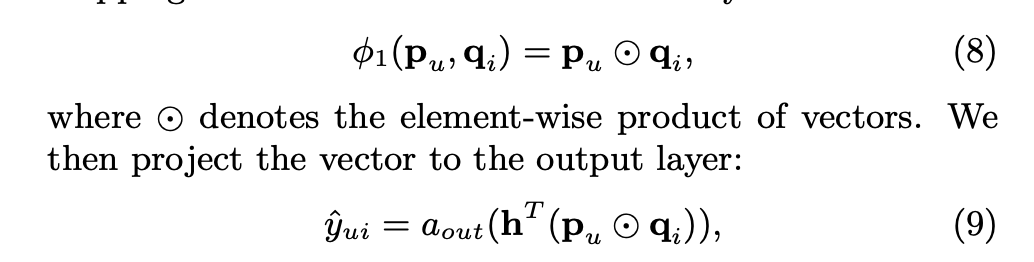
Multi-Layer Perceptron
- MLP라 해서 별거 있는 건 아니고 GMF가 dot-product + 뉴럴넷이라면 MLP는 concat + 뉴럴넷이다.
- GMF 보다는 MLP가 좀 더 user-item interaction을 학습하는 입장에서 flexible함.
- 보통 랭킹 모델의 구조라고 볼 수 있음
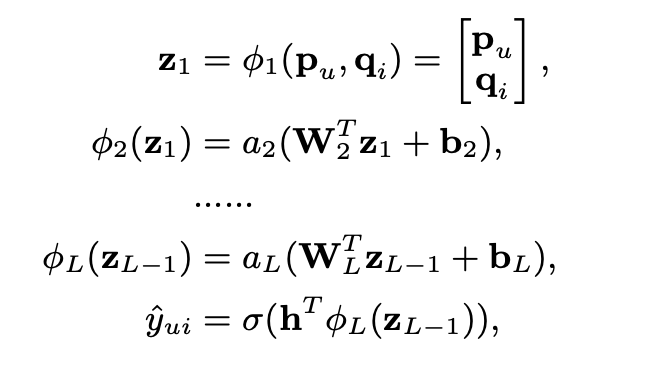
Neural Matrix Factorization
- 위에서 언급한 GMF와 MLP가 각자 다른 특성을 가지고 있는데 이걸 합쳐버리면 더 복잡한 user-item interaction도 표현할 수 있지 않을까?
- 그래서 나온게 다음과 같은 모델 구조. 이렇게 하지 않고 MLP와 GMF가 같은 embedding을 공유할 수 있는데 그렇게 하면 동일한 embedding 사이즈로 고정된다는 단점이 있음. MLP와 GMF를 각각 최적화 했을 때 다른 embedding size를 가질 수 있으므로 분리하는게 더 이상적임
- 수식과 그림은 다음과 같음.
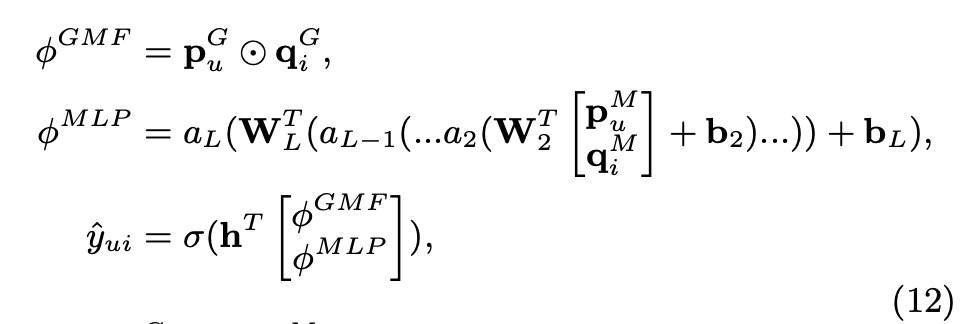
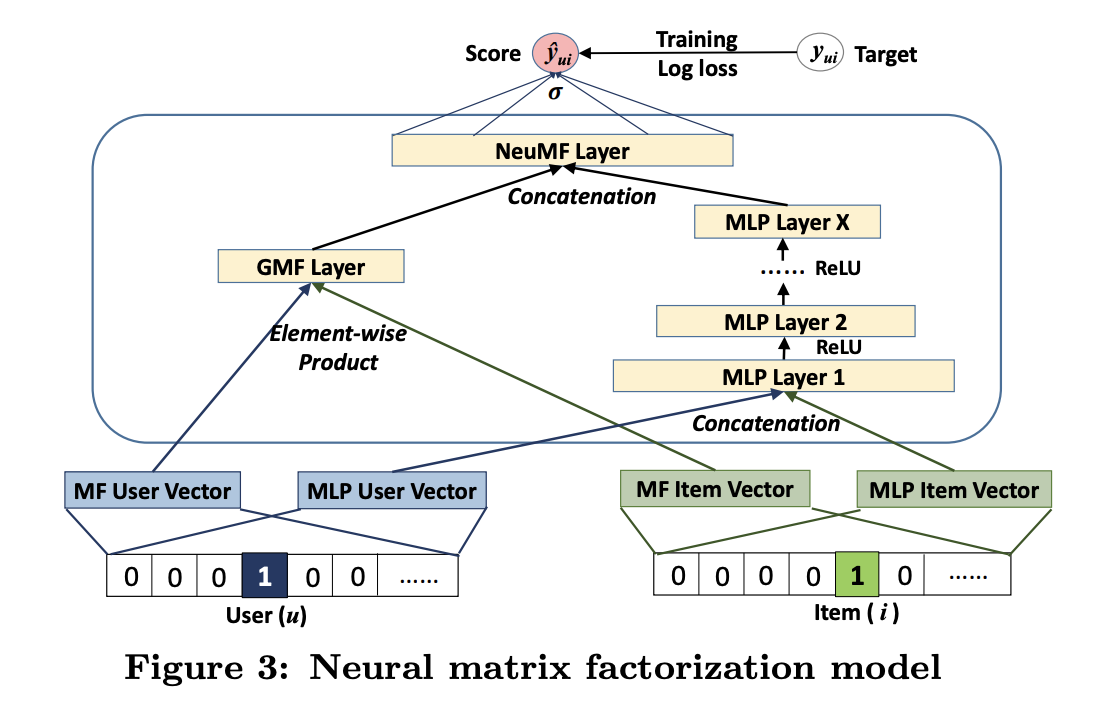
- 마지막에 GMF와 MLP 부분을 합칠 때 weight를 사용해서 trade-off 를 조절할 수 있음. 근데 결국 0.5로 사용함..
- GMF와 MLP를 각각 pretrain 한 다음에(ADAM으로 학습) 합쳐서 NMF로 학습(SGD로 학습)
Experiment
- 학습에 사용한 건 movielense 데이터와 pinterest 데이터.
- 핀터레스트 데이터의 경우 20개의 핀을 본 사용자만 데이터에 포함함.
- 처음 하이퍼 파라메터를 조정하기 위해 사용자 당 하나의 데이터만 추출해서 데이터셋을 만들었음
- 하나의 positive 당 4개의 negative를 뽑아서 학습에 사용함
- 파라메터 초기화는 가우시안 분포로.
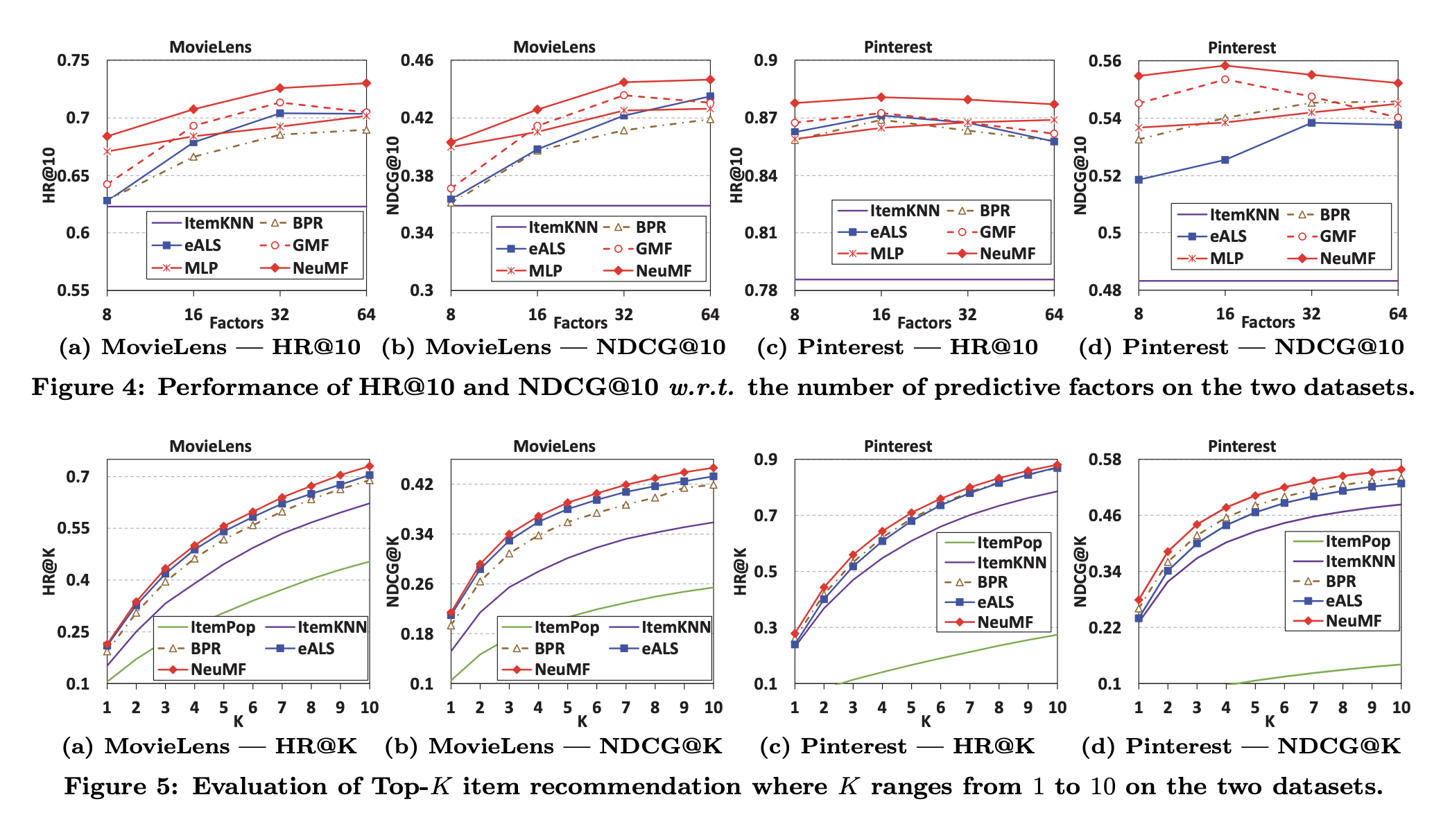
- 핀터레스트 데이터에서 NDCG로 측정할 때는 BPR이 eALS보다 잘 하는 경향이 있음. pair-wise loss를 사용할 경우에 ranking을 잘 하는 경향이 있음
- NeuMF가 모든 경우에 SOTA
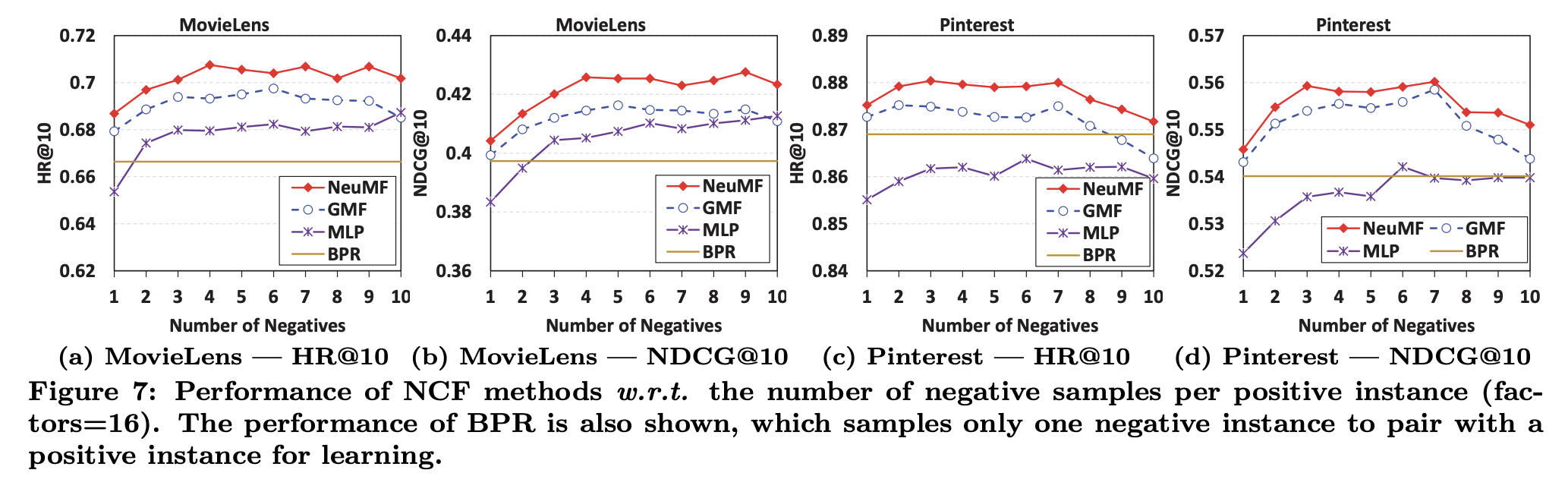
- point-wise loss의 경우 negative sampling ratio를 조절할 수 있다는 장점이 있음. sampling ratio를 조절하면서 실험한 결과는 다음과 같음. 3에서 6 사이가 optimal 함
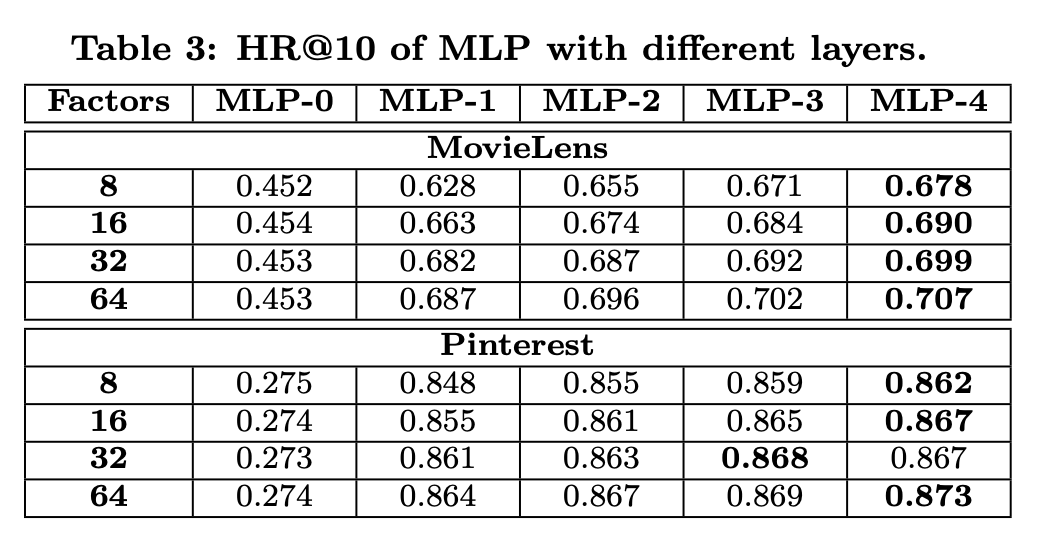
- MLP에서 레이어를 늘리면 더 잘 학습함. 딥러닝 방법이 잘 맞는다는 이야기.
코드
NMF 코드는 논문 저자가 Keras로 구현해놓음. 다음 부분이 모델 부분. NMF 그림과 동일함. GMF의 embedding 차원은 8이고 MLP의 embedding 차원은 32임. MLP의 뉴럴넷 차원은 [64,32,16,8]임.
https://github.com/hexiangnan/neural_collaborative_filtering/blob/master/NeuMF.py
def get_model(num_users, num_items, mf_dim=10, layers=[10], reg_layers=[0], reg_mf=0):
assert len(layers) == len(reg_layers)
num_layer = len(layers) #Number of layers in the MLP
# Input variables
user_input = Input(shape=(1,), dtype='int32', name = 'user_input')
item_input = Input(shape=(1,), dtype='int32', name = 'item_input')
# Embedding layer
MF_Embedding_User = Embedding(input_dim = num_users, output_dim = mf_dim, name = 'mf_embedding_user',
init = init_normal, W_regularizer = l2(reg_mf), input_length=1)
MF_Embedding_Item = Embedding(input_dim = num_items, output_dim = mf_dim, name = 'mf_embedding_item',
init = init_normal, W_regularizer = l2(reg_mf), input_length=1)
MLP_Embedding_User = Embedding(input_dim = num_users, output_dim = layers[0]/2, name = "mlp_embedding_user",
init = init_normal, W_regularizer = l2(reg_layers[0]), input_length=1)
MLP_Embedding_Item = Embedding(input_dim = num_items, output_dim = layers[0]/2, name = 'mlp_embedding_item',
init = init_normal, W_regularizer = l2(reg_layers[0]), input_length=1)
# MF part
mf_user_latent = Flatten()(MF_Embedding_User(user_input))
mf_item_latent = Flatten()(MF_Embedding_Item(item_input))
mf_vector = merge([mf_user_latent, mf_item_latent], mode = 'mul') # element-wise multiply
# MLP part
mlp_user_latent = Flatten()(MLP_Embedding_User(user_input))
mlp_item_latent = Flatten()(MLP_Embedding_Item(item_input))
mlp_vector = merge([mlp_user_latent, mlp_item_latent], mode = 'concat')
for idx in xrange(1, num_layer):
layer = Dense(layers[idx], W_regularizer= l2(reg_layers[idx]), activation='relu', name="layer%d" %idx)
mlp_vector = layer(mlp_vector)
# Concatenate MF and MLP parts
#mf_vector = Lambda(lambda x: x * alpha)(mf_vector)
#mlp_vector = Lambda(lambda x : x * (1-alpha))(mlp_vector)
predict_vector = merge([mf_vector, mlp_vector], mode = 'concat')
# Final prediction layer
prediction = Dense(1, activation='sigmoid', init='lecun_uniform', name = "prediction")(predict_vector)
model = Model(input=[user_input, item_input],
output=prediction)
return model
다음은 negative sampling 하는 부분. 사용자와 positive 아이템을 하나 뽑고 그 사용자와 interaction 하지 않은 아이템들을 가져옴. 이렇게 전체 데이터셋을 만들고 나서 256 batch size로 뽑아서 학습에 사용함.
def get_train_instances(train, num_negatives):
user_input, item_input, labels = [],[],[]
num_users = train.shape[0]
for (u, i) in train.keys():
# positive instance
user_input.append(u)
item_input.append(i)
labels.append(1)
# negative instances
for t in xrange(num_negatives):
j = np.random.randint(num_items)
while train.has_key((u, j)):
j = np.random.randint(num_items)
user_input.append(u)
item_input.append(j)
labels.append(0)
return user_input, item_input, labels
loss function과 optimizer는 다음과 같음
if learner.lower() == "adagrad":
model.compile(optimizer=Adagrad(lr=learning_rate), loss='binary_crossentropy')
elif learner.lower() == "rmsprop":
model.compile(optimizer=RMSprop(lr=learning_rate), loss='binary_crossentropy')
elif learner.lower() == "adam":
model.compile(optimizer=Adam(lr=learning_rate), loss='binary_crossentropy')
else:
model.compile(optimizer=SGD(lr=learning_rate), loss='binary_crossentropy')
